Correction du TD1 de cisaillement

Exercice 1 :

· Question a

Nous faisons l’étude de résistance de la clavette. Celle-ci est soumise à du cisaillement. Nous devons donc d’abord déterminer l’effort qu’elle encaisse. Nous allons faire un équilibre statique du pignon. Nous nous limiterons à l’équation du moment par rapport à l’axe de rotation.

Dans cette équation il faut retrouver la valeur du couple. Par l’intermédiaire de la puissance nous devrions l’obtenir.

On obtient donc :

Pour la détermination de la contrainte nous utilisons

 ; avec cette formule il faut savoir à quoi correspond la section cisaillée de la clavette. Dans l’absolu il n’y a qu’une seule et vraie solution qui est a^.l

· Question b

Nous faisons ici les graphes concernant la clavette. Pour l’effort il est constant. Pour la contrainte en abscisse nous devons choisir l’une des 2 dimensions de la clavette. Nous prendrons l car c’est la seule variable réelle que nous aillons. En effet quand le diamètre de l’arbre est choisi, largeur et hauteur de clavette sont imposées.

Exercice 2 :

· Question a

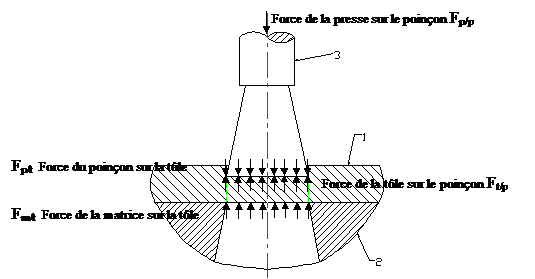Il s’agit ici d’un exercice plus complexe faisant intervenir les caractérisitiques du poinçon et les caractéristiques de la tôle à découper.

Le poinçon doit résister à la compression

La tôle doit céder au cisaillement

A l’équilibre du poinçon nous obtenons un effort normal de cohésion N=F_p/p=F_t/p

Les exposants « p » sont pour préciser qu’il s’agit des caractéristiques du poinçon

A l’équilibre de la tôle nous obtenons un effort de cisaillement de cohésion T=F_p/t=F_m/t

Les exposants « t » sont pour préciser qu’il s’agit des carctéristiques de la tôle

Comme la tôle doit céder nous prenons dans cette inéquation la valeur des caractérisitiques de la tôle que nous multiplions par le cefficient de sécurité car cette valeur n’est en fait qu’un minimum « livrable » par le fournisseur.

Avec les équations on peut donc obtenir en les rapprochant :

soit

une relation entre d,e et les caractéristiques des différents matériaux.

· Question b

Il ne s’agit là que d’une simple application numérique.

Le résultat est