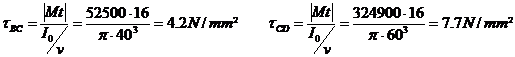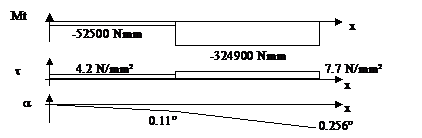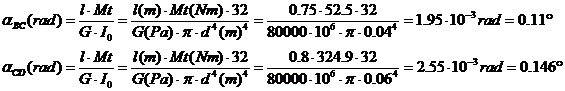Correction du TD1 de torsion

Exercice 1 :

· Question a :

Il s’agit ici d’un exercice de torsion sur un arbre plein.

Les lois, vues en cours, sur cette sollicitation peuvent donc être appliquées. On recherche ici le diamètre minimum qui permettra de résister aux actions mécaniques extérieures. On va donc utiliser :

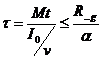
Dans cette inéquation nous avons besoin de Mt. Si nous avions fait une coupe fictive entre l’accouplement et l’hélice en introduisant le torseur de cohésion, nous aurions trouvé Mt=C. Où C représente le couple fourni par le moteur.

Nous pouvons maintenant appliquer directement l’inéquation précédente et déterminer la valeur de d minimale.

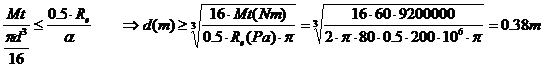
· Question b :

Pour répondre à cette question nous allons utiliser l’équation de déformation.

Soit une valeur en degré de : pour les 3 mètres de longueur de l’arbre.

· Question c :

Ici la déformation angulaire unitaire est limitée. Nous allons donc réutiliser l’équation précédente mais en cherchant d.

Il faudrait alors prendre pour respecter cette hypothèse de déformation maxiamale admissible un diamètre d’arbre supérieur à 532mm.

Exercice 2 :

· Question a :

Dans un premier temps il faut déterminer les actions CT et Ct. Pour cela nous allons faire une petite étude statique sans tenir compte des paliers.

Par rapport au sujet nous placons le repère suivant :

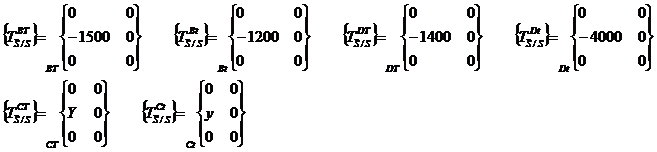
Nous pourrions faire une étude statique complète, mais il ne s’agit ici pas du vrai problème. Nous allons donc nous limiter à l’étude du moment sur l’axe x et la projection des efforts sur l’axe y.

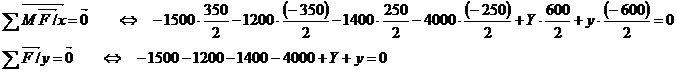
En résolvant ces deux équations on obtient Y=3596 N et y=4504N. Donc en reprenant le sujet, on retrouve pour CT=3596 N et pour Ct =4504 N.

· Question b :

On est là maintenant dans un problème de RdM mais nous allons vérifier qu’il s’agit bien d’une sollicitation de torsion.

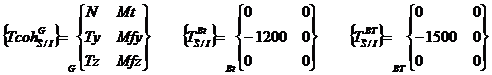
Transport au point G des 2 torseurs d’AME.

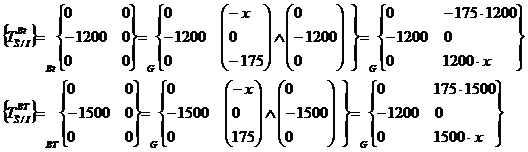
On fait le PFD en G et l’on trouve 3 sollicitations. Du cisaillement sur y et de la flexion sur z que nous allons négliger. Mais également de la torsion.

On peut appliquer les lois sur la torsion et déterminer le diamètre minimum de la zone BC, à savoir :

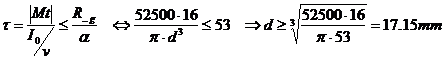
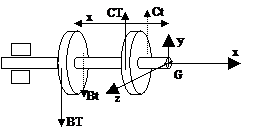Par analogie on refait le même travail mais en faisant une coupe fictive entre C et D.

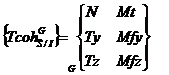
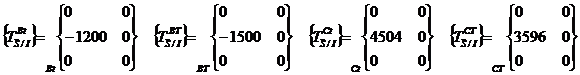
Transport au point G des 2 nouveaux torseurs d’AME.

On trouvera alors :

On peut appliquer les lois sur la torsion et déterminer le diamètre minimum de la zone CD, à savoir :

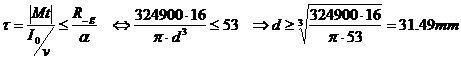
· Question c :

On va ici utiliser la formule de déformation.

Dans la zone BC on a :

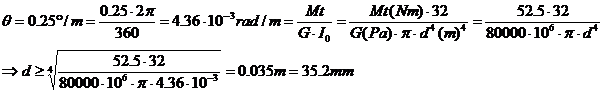
Dans la zone BC on a :

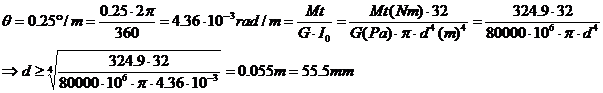
· Question d :

Il faut refaire les calculs pour la contrainte et calculer non pas q mais a. Pour le graphe des moments il ne change pas il faut juste le tracer avec les valeurs déjà trouvées.