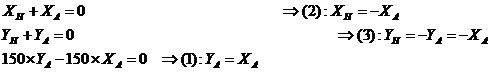Correction
du Contrôle 3 de statique GIM1
Réponse 1 : Transport d’un
torseur
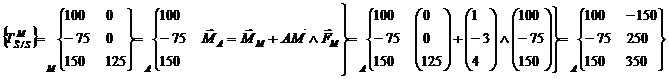
Réponse 2 : Connaissance des liaisons
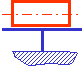
Rotule Appui
plan de normale x Linéaire rectiligne d’axe z
z z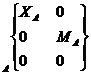
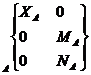
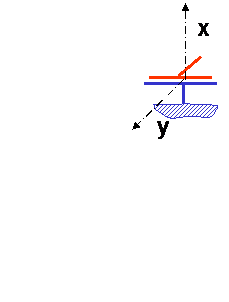
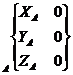
Réponse 3 : Connaissance des torseurs
Il n’existe qu’une seule liberté et il s’agit d’un déplacement linéaire sur l’axe x il faut donc trouver une liaison qui annule 5 degrés de liberté et laisse un déplacement linéaire sur x è il s’agit d’une liaison glissière.
x
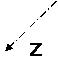
Problème 4 :
Réponse a : Frontières, repère
Il faut d’abord donner les limites de l’étude à savoir : 1 ; 3 ; 4 ; 5
Le repère choisi est plan avec l’axe horizontal porté par x et l’axe vertical par y
Toutes les liaisons sont des rotules et en C on a une AME.
Réponse b : Graphe de liaisons
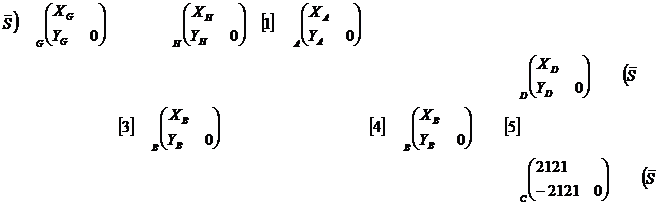
Réponse c : Résolvabilité
On doit répondre à la question n x E ≥ I
E = 3 n = 4 I = 12
Donc le problème est résolvable et isostatique.
Réponse d : Comment trouver le plus rapidement
possible la tension dans la barre 1
Cela revient à trouver XA et YA
Inventaire « exhaustif des études réalisables »
Système composé d’un seul solide : 1 3 4 5
Système composé de 2 solides : 1U3 1U4 3U4 4U5
Système composé de 3 solides : 1U3U4 1U4U5 3U4U5
Système composé de 4 solides : Tout
Repérage des solides ou systèmes soumis à 2 torseurs de type Rotule ou Ponctuelle.
On a 1, et 1U3U4.
On en fera donc l’étude en premier.
Etude A : solide 1 è tout sera exprimé en fonction d’une unique inconnue par exemple XA ;
Etude B : système 1U3U4 è tout sera exprimé en fonction d’une unique inconnue par exemple XB ;
Reprise de l’inventaire exhaustif
et suppression des études inutiles
Avec solide particulier en périphérie on retire : 1U3 1U4 1U4U5 Tout
Avec solide
particulier « entrant/sortant » on retire : 3U4
Tableau récapitulatif :
|
Système |
Inconnues |
S des I |
E |
Conclusion |
|
3 |
XE ; YE ; XA ; XB |
4 |
3 |
Irrésolvable |
|
4 |
XE ; YE ; XA ;
XB |
4 |
3 |
Irrésolvable |
|
5 |
XB ;
XD ; YD |
3 |
3 |
Résolvable |
|
4U5 |
XA ;
XE ; YE ; XD ;
YD |
5 |
3 |
Irrésolvable |
|
3U4U5 |
XD ;
YD ; XA ; XB |
4 |
3 |
Irrésolvable |
L’étude C du solide 5 permet donc de trouver numériquement 3 inconnues XB ; XD ; YD. Reste alors le tableau suivant :
|
Système |
Inconnues |
S des I |
E |
Conclusion |
|
3 |
XE ; YE ; XA |
3 |
3 |
résolvable |
|
4 |
XE ; YE ; XA |
3 |
3 |
résolvable |
|
4U5 |
XA ;
XE ; YE |
3 |
3 |
résolvable |
|
3U4U5 |
XA |
1 |
3 |
résolvable |
On peut donc choisir l’étude que l’on veut. On choisira le solide 3 car il possède le moins de torseurs et sa géométrie (horizontale) devrait faciliter les calculs…
Récapitulatif pour trouver XA
et YA :
Etude A : solide 1 è tout sera exprimé en fonction d’une unique inconnue par exemple XA ;
Etude B : système 1U3U4 è tout sera exprimé en fonction d’une unique inconnue par exemple XB ;
Etude C : solide 5 è résultats numériques pour XB ; XD ; YD ;
Etude D : solide 3 è résultats numériques pour XE ; YE ; XA.
Réponse e : Etude A du solide 1
Inventaire des torseurs
Choix d’un point d’application pour pouvoir appliquer le PFD : H
Transport des torseurs au point H
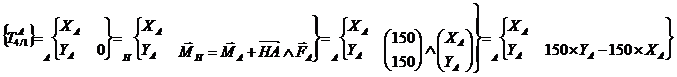
Résolution
Conclusion
Etude B du système 1U3U4
Inventaire des torseurs
Choix d’un point d’application pour pouvoir appliquer le PFD : G
Transport des torseurs au point G
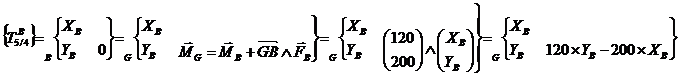
Résolution
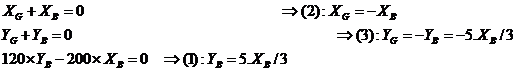
Conclusion
Etude C du solide 5
Inventaire des torseurs
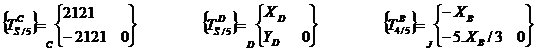
Choix d’un point d’application pour pouvoir appliquer le PFD : D
Transport des torseurs au point D
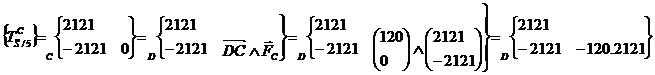
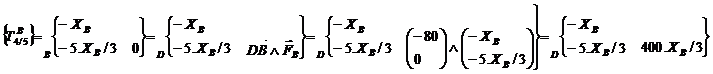
Résolution
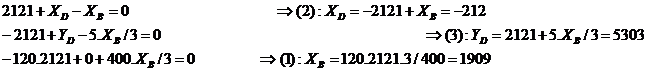
Conclusion
Etude D du solide 3
Inventaire des torseurs
Choix d’un point d’application pour pouvoir appliquer le PFD : E
Transport des torseurs au point E
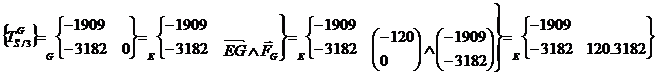
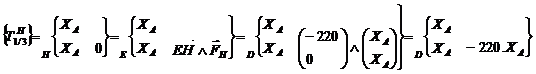
Résolution
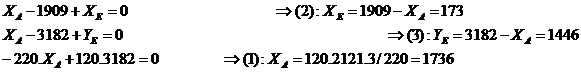
Conclusion
Réponse 6 : tension dans la barre 1
Il faut juste calculer le module de la force en A soit :
