Correction DS 6 rameur en statique

Fondamentaux :

Q1 :

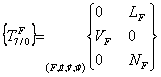
Q2 :

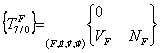
Q3 :

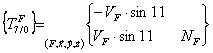
Problème électif :

Q4 :

· Système de repère utilisé :

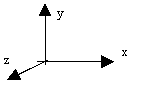
· Le problème est de type plan, les torseurs seront représentés par leur résultante sur et et leur moment sur .

· Les limites de l’étude sont les pièces 1, 2, 3, 4, 5, 6, 7 et 8.

· Graphe de liaisons :

Q5 :

Le nombre de solide est n et vaut : 8

Le nombre d’équations est E et pour un système plan vaut : 3

Le nombre d’inconnues est I et vaut : 24

E*n = I è On a donc un système isostatique et surtout réalisable.

Q6 :

· Dans la mesure où l’on doit déterminer l’ensemble des actions mécaniques il convient pour arriver le plus rapidement à des résultats numériques et pour éviter d’écrire des fonctions de fonctions d’étudier les systèmes soumis à deux torseurs de type rotules ou ponctuelles. On peut donc étudier successivement :

Etude A : solide 1=> tout en fonction d’une unique inconnue (par exemple X_A)

Etude B : solide 3=> tout en fonction d’une unique inconnue (par exemple X_D)

Etude C : solide 8=> tout en fonction d’une unique inconnue (par exemple X_K)

Etude D : système 5U6U8 => tout en fonction d’une unique inconnue (par exemple X_J)

· Après étude des systèmes soumis à 2 torseurs on obtiendra :

· Inventaire exhaustif des études réalisables

1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 1U2 ; 2U3 ; 3U4 ; 4U7 ; 7U6 ; 6U8 ; 6U5 ; 8U5 ; 1U2U3 ; 2U3U4 ; 3U4U7 ; 4U7U6 ; 7U6U8 ; 7U6U5 ; 6U8U5 ; 1U2U3U4 ; 2U3U4U7 ; 3U4U7U6 ; 4U7U6U8 ; 4U7U6U5 ; 7U6U8U5 ; 1U2U3U4U7 ; 2U3U4U7U6 ; 3U4U7U6U5 ; 3U4U7U6U8 ; 4U7U6U8U5 ; 1U2U3U4U7U6 ; 2U3U4U7U6U8 ; 2U3U4U7U6U5 ; 3U4U5U6U7U8 ; 1U2U3U4U6U8U7 ; 1U2U3U4U5U6U7 ; 2U3U4U5U6U7U8 ; 1U2U3U4U5U6U7U8

Sur les 42 études possibles on peut supprimer 31 qui sont soit :

· Des systèmes déjà étudiés (Etude A à D)

· Des étudesqui en termes d’inconnues ont déjà été réalisées (système à verrue) par exemple 1U2 qui est ó à 2

· Des études où les verrues rentrent et sortent, par 5U6 avec 8 en verrue.

Il ne reste donc que 11 lignes maxi dans le tableau de synthèse avec : 2 ; 4 ; 5 ; 6 ; 7 ; 4U7 ; 7U6 ; 2U3U4 ; 4U7U6 ; 2U3U4U7 ; 2U3U4U7U6

· Tableau récapitulatif des études menables pour résoudre au plus vite le problème :

Système isolé	Inconnues	Is	Es	Conclusion
2	XA ; XD ; XC ; YC	4	3	Irrésolvable
4	XD ; XF4 ; YF4	3	3	Réalisable

L’étude E du solide 4 permet de trouver des solutions numériques. On trouve donc XD et par conséquent le solide 2 en étude F est réalisable et donne des solutions numériques.

On peut continuer le tableau :

Système isolé	Inconnues	Is	Es	Conclusion
7	NF ; NF ; XJ	3	3	Résolvable
6	XK ; XH ; YH	3	3	Résolvable

Les deux études sont réalisables et permettent d’arriver à connaître l’ensemble des inconnues restantes.

L’étude globale du système donne donc :

Etude A : Solide 1 Etude E : Solide 4

Etude B : Solide 3 Etude F : Solide 2

Etude C : Solide 8 Etude G : Solide 7

Etude D : Système 5U6U8 Etude H : Solide 6

Q7 :

Etude du solide 1

· Inventaire des torseurs :

· PFD :

· Choix du point d’étude : A, on placera alors le repère en ce point

· Transport des torseurs au point d’étude :

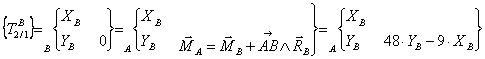
· Application du PFD :

· Résumé des torseurs obtenus :

Q8 :

· Le vérin amortisseur développe 250 N dans sa valeur minimale. On aura donc :

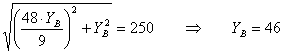
En remplacant dans le torseur en B on obtient :

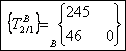
Il faut aussi faire l’étude de la barre 3 pour lier XD et YD.

Etude du solide 3

· Inventaire des torseurs :

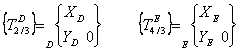
· PFD :

· Choix du point d’étude : D

· Transport des torseurs au point d’étude :

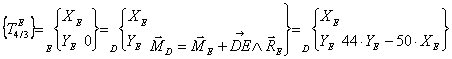
· Application du PFD :

· Résumé des torseurs obtenus :

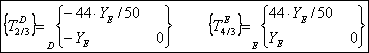
Etude du solide 2

· Inventaire des torseurs :

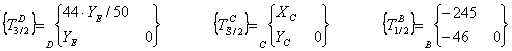
· PFD :

· Choix du point d’étude : C

· Transport des torseurs au point d’étude :

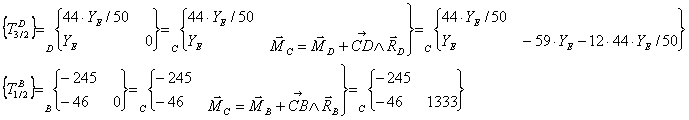
· Application du PFD :

· Résumé des torseurs obtenus :

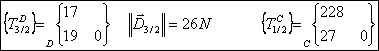
Q9 :

Il faut juste rajouter le muscle détendu entre 4 et 6 et lui donner une raideur sinon le système n’est pas stable.