Correction du Devoir Surveillé de Statique et RdM n° 7

Question 1 :

· Repère utilisé :

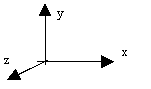
· Le problème est de type plan, les torseurs seront représentés par leur résultante sur et et leur moment sur .

· Les limites de l’étude sont les pièces 1, 2U4 et 3. En effet les roues seront associées au bâti mobile 2.

· Graphe de liaisons :

Question 2 :

· Inventaire des inconnues :

Is = 8 n = 3 Es = 3

n*Es = 9 Is<n*Es ==> Système résolvable et hypostatique.

· Dans la mesure où l’on doit déterminer l’ensemble des actions mécaniques il convient pour arriver le plus rapidement à des résultats numériques et pour éviter d’écrire des fonctions de fonctions d’étudier les systèmes soumis à deux torseurs. Ici il n’y a que le solide 3 et l’on exprimera tout en fonction d’une unique inconnue (par exemple : X_D).

· Représentation du graphe de liaison après étude de 3 :

On étudiera donc en premier lieu le solide soumis à deux torseurs soit :

Etude A : le solide 3, tout en fonction de X_D.

· Inventaire exhaustif des études réalisables

1 ; 3 ; 2U4 ; 1U3 ; 1U2U4 ; 3U2U4 ; 1U3U2U4

3 est déjà réalisée, 1U3ó1, 2U4U3ó2U4

1U2U4 est inintéressant car 3 est entrant et sortant

· Tableau récapitulatif des études menables pour résoudre au plus vite le problème :

Système isolé	Inconnues	Is	Es	Conclusion
1	XA ; YA ; XD	3	3	Résolvable
2U4	YE ; YF ;XA ; YA ; XD	5	3	Irrésolvable
1U2U3U4	YE ; YF	2	3	Résolvable

Pour l’étude B deux systèmes sont résolvables. Le solide 1 qui permet de déterminer numériquement les inconnues X_A, Y_A et X_D et le système 1U2U3U4 qui lui permet de déterminer Y_E et Y_F. Les 5 inconnues sont différentes.

Il en résulte donc :

Etude B : le solide 1

Etude C : le système 1U2U3U4

L’étude globale du système donne donc :

Etude A : le solide 3, tout en fonction de X_D.

Etude B : le solide 1 avec des résultats numériques pour X_A, Y_A et X_D

Etude C : le système 1U2U3U4 avec des résultats numériques pour Y_E et Y_F.

Question 3 :

Pour déterminer la pression nécessaire il faut connaître l’effort appliqué au point B. On doit donc réaliser les études A et B.

Etude A : solide 3

· Inventaire des torseurs :

· Principe Fondamental de la Dynamique appliqué à un système statique :

· Choix du point d’étude : D, on placera alors le repère en ce point.

· Transport des torseurs au point d’étude :

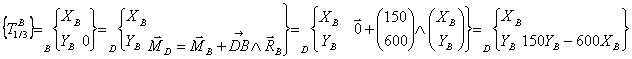
· Application du PFD :

· Résumé des torseurs obtenus :

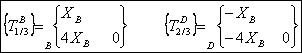
Etude B : solide 1

· Inventaire des torseurs :

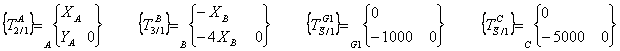
· PFD :

· Choix du point d’étude : A

· Transport des torseurs au point d’étude :

· Application du PFD :

· Résumé des torseurs obtenus :

· Réponse à la question posée sur la pression minimale :

Question 4 :

En faisant l’étude de l’ensemble on trouvera les valeurs de Y_E et Y_F. Il y aura basculement si Y_E=0.

Etude du système 1U2U3U4 = S

· Inventaire des torseurs :

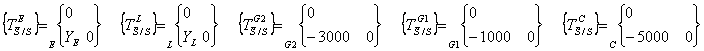
· PFD :

· Choix du point d’étude : A car certains calculs ont déjà été réalisés en ce point.

· Transport des torseurs au point d’étude :

· Application du PFD :

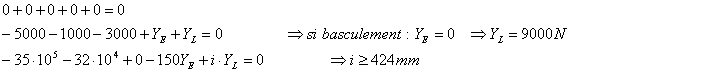Conclusion sur la question :

Donc si i est supérieur à 424mm il n’y aura pas de basculement de la grue sous cette charge.

Question 5 :

On est ici dans une sollicitation de compression pure. On utilise donc les trois équations suivantes :

Une simple application numérique permet d’obtenir la valeur minimale pour d :

Question 6 :

Pour le raccourcissement il en est de même, il faut juste remarquer que le matériau utilisé est de l’acier et que donc son module d’élasticité longitudinale E vaut 210000MPa.

Il faut évidement utiliser le diamètre proposé et non utiliser la contrainte limite admissible par le matériau.

On obtient alors :

Question 7 :

L’axe 5 est soumis a du cisaillement, il faut donc utiliser ses caractéristiques de glissement. Il faut également remarquer que deux sections de cet axe résistent au cisaillement.

Par une application numérique on obtient alors :

Question 8 :

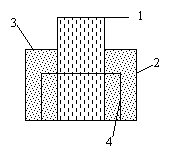
Pour déterminer le CdG il faut décomposer en surfaces élémentaires et appliquer les formules du barycentre.

Il est évident que X_G = 40 puisque la pièce possède un axe de symétrie verticale.

i	xGi	yGi	Si	xGi. Si	yGi.Si
1	40	75	4500	180000	337500
2	67.5	50	2500	168750	125000
3	12.5	50	2500	31250	125000
4	40	30	-3600	-144000	-108000
total			5900	236000	479500
XG=S xGi. Si/S Si			40
YG=S yGi. Si/S Si			81,27

Pour le calcul du moment quadratique on peut utiliser le même découpage. Chaque surface est en contact avec l’axe x et l’on peut donc utiliser :

On obtient alors :

Il ne reste plus qu’à utiliser Huyghens pour avoir l’inertie I_GX.

Question 9 :

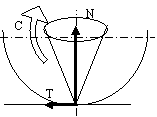La force normale N au contact équivalente vaut donc 9000N. En représentant le cône d’adhérence autour de cette force on obtient d’après la loi de Coulomb une force tangentielle de T=Nf ou f est le coefficient de frottement. L’application numérique donne alors T=4500N. Le couple nécessaire est alors C=T.r ou r est le rayon de la roue. L’application numérique donne :