Correction de la Grue de Garage

Question 1 :

· Repère utilisé :

· Le problème est de type plan, les torseurs seront représentés par leur résultante sur et et leur moment sur .

· Les limites de l’étude sont les pièces 1, 2U4 et 3. En effet les roues seront associées au bâti mobile 2.

· Graphe de liaisons :

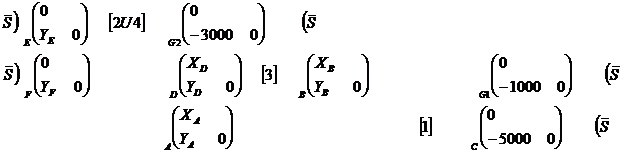
Question 2 :

· Inventaire des inconnues :

Is = 8 n = 3 Es = 3

n*Es = 9 Is<n*Es ==> Système résolvable et hypostatique.

· Dans la mesure où l’on doit déterminer l’ensemble des actions mécaniques il convient pour arriver le plus rapidement à des résultats numériques et pour éviter d’écrire des fonctions de fonctions d’étudier les systèmes soumis à deux torseurs. Ici il n’y a que le solide 3 et l’on exprimera tout en fonction d’une unique inconnue (par exemple : X_D).

· Représentation du graphe de liaison après étude de 3 :

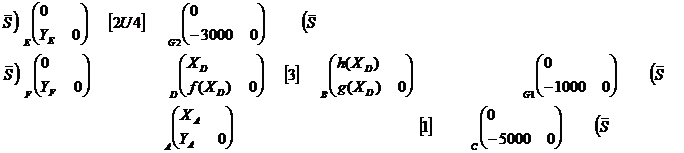
On étudiera donc en premier lieu le solide soumis à deux torseurs soit :

Etude A : le solide 3, tout en fonction de X_D.

· Inventaire exhaustif des études réalisables

1 ; 3 ; 2U4 ; 1U3 ; 1U2U4 ; 3U2U4 ; 1U3U2U4

3 est déjà réalisée, 1U3ó1, 2U4U3ó2U4

1U2U4 est inintéressant car 3 est entrant et sortant

· Tableau récapitulatif des études menables pour résoudre au plus vite le problème :

Système isolé	Inconnues	Is	Es	Conclusion
1	XA ; YA ; XD	3	3	Résolvable
2U4	YE ; YF ;XA ; YA ; XD	5	3	Irrésolvable
1U2U3U4	YE ; YF	2	3	Résolvable

Pour l’étude B deux systèmes sont résolvables. Le solide 1 qui permet de déterminer numériquement les inconnues X_A, Y_A et X_D et le système 1U2U3U4 qui lui permet de déterminer Y_E et Y_F. Les 5 inconnues sont différentes.

Il en résulte donc :

Etude B : le solide 1

Etude C : le système 1U2U3U4

L’étude globale du système donne donc :

Etude A : le solide 3, tout en fonction de X_D.

Etude B : le solide 1 avec des résultats numériques pour X_A, Y_A et X_D

Etude C : le système 1U2U3U4 avec des résultats numériques pour Y_E et Y_F.