|
Correction du demi pont arrière de véhicule |
Question
1 :
· Système
de repère utilisé :

· Le
problème est de type plan, les torseurs seront représentés par leur résultante
sur ![]() et
et ![]() et leur moment sur
et leur moment sur ![]() .
.
· Les
limites de l’étude sont les pièces 1, 2, 3, 4 et 10.
·
Graphe de liaisons :

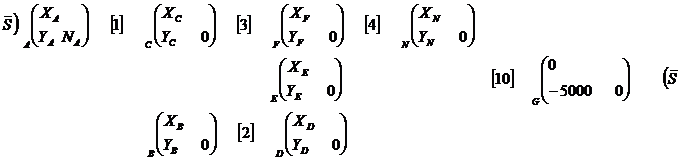
· Inventaire
des inconnues :
Is = 15 n
= 5 Es
= 3
n*Es
= 15 Is=n*Es ==> Système
résolvable et isostatique.
Question 2 :
·
Dans la mesure où l’on doit
déterminer l’ensemble des actions mécaniques il convient pour arriver le plus
rapidement à des résultats numériques et pour éviter d’écrire des fonctions de
fonctions d’étudier les systèmes soumis à deux torseurs.
·
Etude des systèmes soumis à 2
torseurs et leur simplification

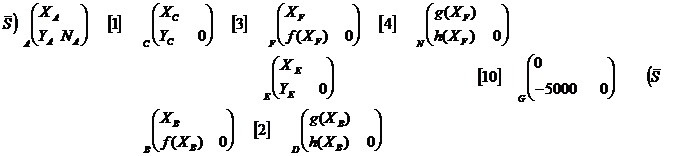
Le graphe
précédent représente la solution de principe des deux études suivantes.
On étudiera
donc en premier lieu les deux solides soumis à deux torseurs soit :
Etude A : le solide 2,
tout en fonction de XB.
Etude
B : le solide 4, tout en fonction de XF.
·
Inventaire exhaustif des études
réalisables
1 ; 2 ; 3 ; 4 ; 10 ;
1U3 ; 1U2 ; 3U4 ; 4U10 ; 3U10 ; 2U10 ;
1U3U4 ; 3U4U10 ; 1U3U10 ;
1U2U3 ; 3U10U2 ; 4U10U2 ;
1U3U4U10 ; 4U3U1U2 ; 3U4U10U2 ;
1U2U3U4U10
2 et 4 sont déjà réalisées, 1U2ó1, 3U4ó3, 4U10ó10, 2U10ó10, 1U3U4ó1U3, 1U2U3ó1U3, 3U10U2ó3U10, 4U10U2ó10, 4U3U1U2ó1U3, 3U4U10U2ó3U4U10
1U3U10, 3U10, sont inintéressants car 4 est I&O
1U3U4U10 est
inintéressant car 2 est I&O
·
Tableau récapitulatif des études menables pour résoudre au plus vite le problème :
|
Système
isolé |
Inconnues |
Is |
Es |
Conclusion |
|
1 |
XA ;
YA ; NA ; XC ; YC ; XB |
6 |
3 |
Irrésolvable |
|
3 |
XE ;
YE ; XC ; YC ; XF |
5 |
3 |
Irrésolvable |
|
10 |
XF ; XB ; XE ; YE |
4 |
3 |
Irrésolvable |
|
1U3 |
XA ; YA ; NA ;
XE ; YE ; XB ; XF |
7 |
3 |
Irrésolvable |
|
3U4U10 |
XC ; YC ; XB |
3 |
3 |
Résolvable |
|
1U2U3U4U10 |
XA ; YA ; NA |
3 |
3 |
Résolvable |
Pour
l’étude C deux systèmes sont résolvables. Le système
3U4U10 qui permet de déterminer numériquement les inconnues XC, YC et XB et le
système 1U2U3U4U10 qui lui permet de déterminer XA, YA et NA. Les 6 inconnues
sont différentes.
Il en résulte donc :
Etude C : le système 3U4U10
Etude D : le système 1U2U3U4U10
Le tableau résultant présente alors la
forme suivante :
|
Système
isolé |
Inconnues |
Is |
Es |
Conclusion |
|
1 |
Plus d’inconnue |
0 |
3 |
Inutile |
|
3 |
XE ;
YE ; XF |
3 |
3 |
Résolvable |
|
10 |
XF ; XE ; YE |
3 |
3 |
Résolvable |
|
1U3 |
XE ; YE ; XF |
3 |
3 |
Résolvable |
Les
trois études permettent de trouver les trois dernières inconnues restantes. On
choisira d’étudier 3 qui présente le moins de torseurs
à étudier.
Etude E : le solide 3.
L’étude globale du système donne
donc :
Etude A :
solide 2, tout en fonction de XB.
Etude B :
solide 4, tout en fonction de XF.
Etude C :
système 1U2U3U4 qui permet de déterminer : XC, YC, XB
Etude D :
système 1U2U3U4U10 qui permet de déterminer : XA, YA,
NA
Etude E :
solide 3 qui permet de déterminer : XE, YE, YF
Question 3 :
|
Etude
du solide 2 |
·
Inventaire des torseurs :
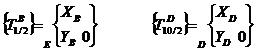
·
Principe Fondamental de la Dynamique
appliqué à un système statique :
![]()
·
Choix du point d’étude : B, on
placera alors le repère en ce point.
·
Transport des torseurs au point
d’étude :
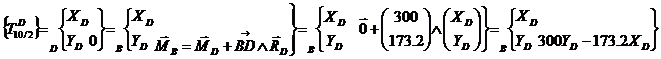
·
Application du PFD :
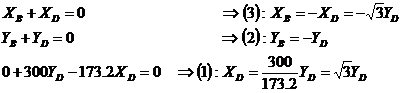
·
Résumé des torseurs obtenus :
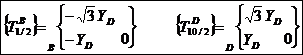
Question 4 :
|
Etude du système 1U2U3U4U10 =
S |
·
Inventaire des torseurs :
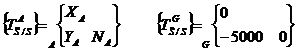
·
PFD :
![]()
·
Choix du point d’étude : A
·
Transport des torseurs au point
d’étude :
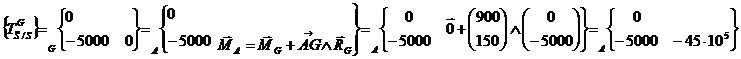
·
Application du PFD :
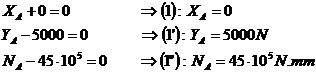
·
Résumé des torseurs obtenus :
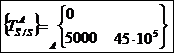
Question 5 :
L’objectif
est ici différent il faut trouver une valeur particulière, en l’occurrence la
valeur de l’effort dans la barre 2. Nous allons donc reprendre les tableaux et
voir ce qui nous permettra de la trouver le plus rapidement possible.
L’étude
du solide 2 est bien évidement indispensable mais reste non réalisable en terme d’application numérique. Tout sera donc écrit en
fonction d’une unique inconnue par exemple : XB.
·
Ensuite on peut refaire le graphe
de liaison suivant :

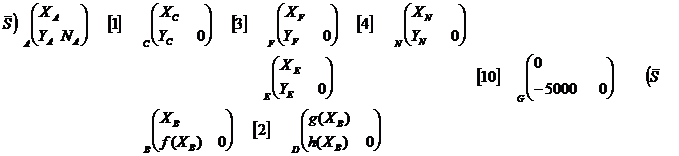
·
Tableau récapitulatif des études menables pour résoudre au plus vite le problème :
|
Système
isolé |
Inconnues |
Is |
Es |
Conclusion |
|
1 |
XA ;
YA ; NA ; XC ; YC ; XB |
6 |
3 |
Irrésolvable |
|
10 |
XN ; YN ; XB ;
XE ; YE |
5 |
3 |
Irrésolvable |
|
1U3 |
XA ; YA ; NA ;
XE ; YE ; XB ; XF ; YF |
8 |
3 |
Irrésolvable |
|
3U4U10 |
XC ; YC ; XB |
3 |
3 |
Résolvable |
|
1U2U3U4U10 |
XA ; YA ; NA |
3 |
3 |
Résolvable |
Pour répondre
à la question il y a deux méthodes. La première est d’utiliser les études déjà
réalisées et alors nous obtenons :
Etude A :
solide 2 tout en fonction de XB
Etude B :
1U2U3U4U10, nous trouvons des valeurs numériques pour XA, YA et NA.
Etude C :
solide 1, nous trouvons des valeurs numériques pour XC, YC et XB.
La seconde
méthode et certainement la meilleure si nous repensons le problème directement
au niveau de la question 5 est :
Etude A :
solide 2 tout en fonction de XB
Etude B :
solide 3U4U10, nous trouvons des valeurs numériques pour XC, YC et XB.
|
Etude
du système 3U4U10 = S |
·
Inventaire des torseurs :
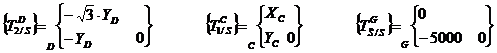
·
PFD :
![]()
·
Choix du point d’étude : C
·
Transport des torseurs au point
d’étude :
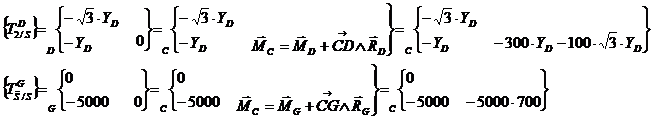
·
Application du PFD :
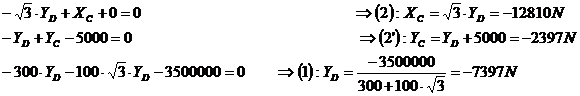
·
Résumé des torseurs obtenus :
![]()
· Réponse
à la question :
L’action exercée sur la barre 2 est donc
en D :
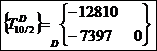
Il s’agit bien sur d’une compression
dont l’intensité est :
![]()